The simple conceptual logic of Mechanistic models of brains
Brains, Networks, Neurons, Channels, Molecules, and Physics
Summer schools are where much of the cutting-edge learning of new concepts in neuroscience happens (check out Neuromatch Academy, of which I am a co-founder). During a summer school in Germany, Peter König—my future PhD supervisor—introduced me to one of the first systems neuroscience papers I read: “Role of the temporal domain for response selection and perceptual binding.1” The paper speculated that the brain solves a specific problem—determining which pieces of information belong together as parts of the same object—and it raised the question: how do individual neurons and circuits interact to achieve this binding? By how, we mean here the question of how neurons can interact with one another so that the problem gets solved and today I will talk about the logic of these kinds of models (see Neuromatch academy D1 as well).
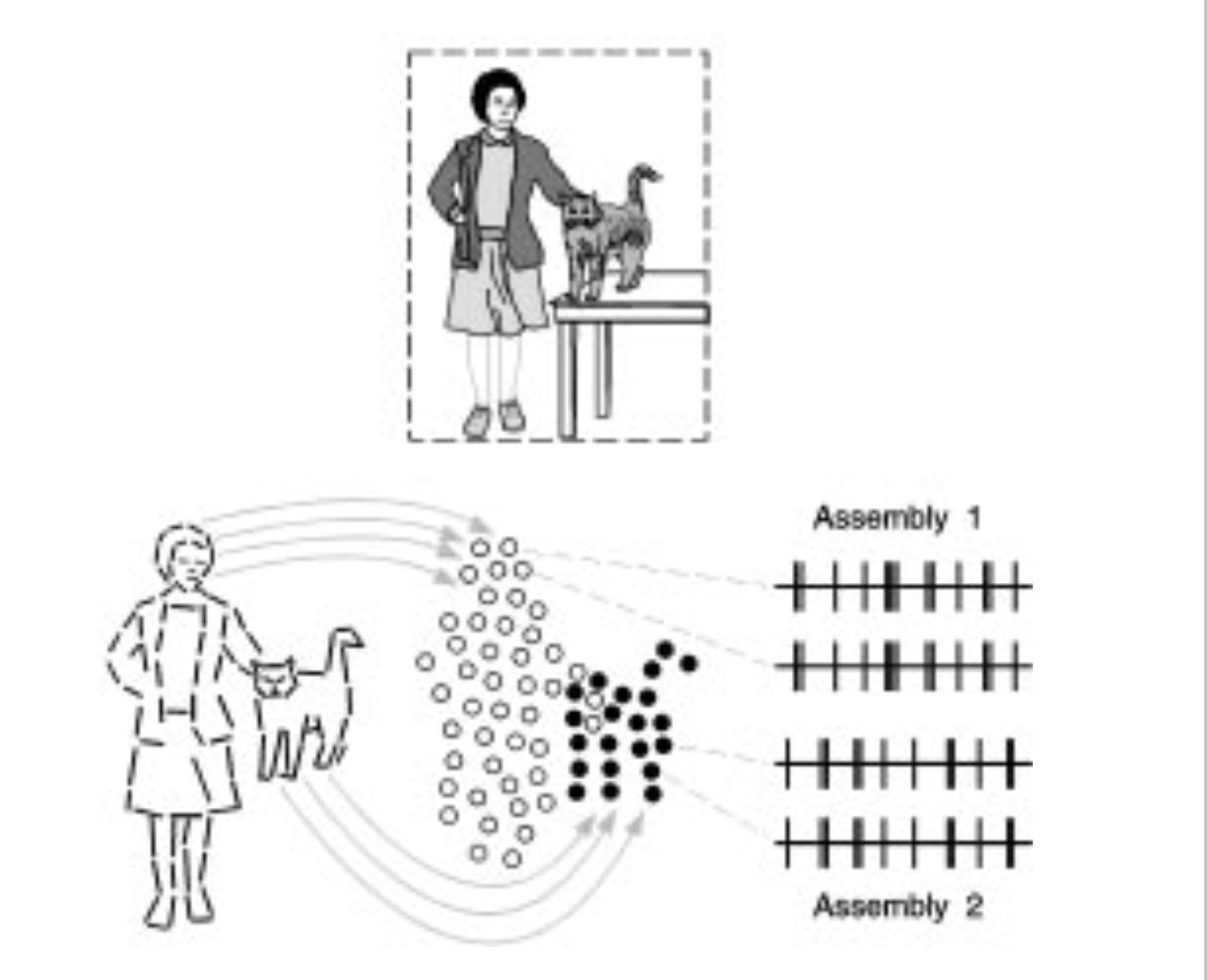
We call these models mechanistic in the sense that they hypothesize specific, testable causal interactions among neurons and circuits that produce measurable phenomena in the real brain, and that we understand the components of these pathways. We can also call them reductionist in the sense that they take one level of the system’s behavior (tagging what belongs together) and explain it in terms of a lower-level variable (the interaction between neurons). Some people simply call them “how models”. This blog post is about the logic of these mechanistic/ causal/ reductionist/ how models.
The logic of mechanistic models
Canonical phenomenon at one level of the brain. We assume there are some canonical properties that a system has. For example, a pyramidal neuron in the neocortex typically spikes—rapidly depolarizing and then hyperpolarizing—which allows action potentials to propagate along its axon. This allows spikes to travel along the axons. This phenomenon might manifest as an animal behavior (such as retracting when poked), a property of a brain region (like stability), or as an intrinsic characteristic of a neuron (for example, spiking activity). In typical successful cases, this is a small, circumscribed phenomenon but it can also be large-scale (e.g. recognizing a hand). Key is that there is something happening at a given level that we want to understand the mechanism of.
Example of a phenomenon to be explained. A neuron spiking. A reductive assumption: larger phenomena arise from interactions of smaller ones. The phenomenon of interest arises because of interactions of things at a lower level. For example, a neuron spiking may be due to a set of interactions between cell voltage and ion channels. Or I might recognize a hand due to a set of interactions between activities across neurons. The key is that if we could understand these smaller-scale interactions, we would be able to understand the larger-scale behavior.
Sodium and potassium channels as components of spiking. These interactions are generally assumed to be parsimonious and form an understandable model. The interactions at a lower level are assumed more understandable than interactions at a higher level, partly because fewer components are involved or the system is more constrained.
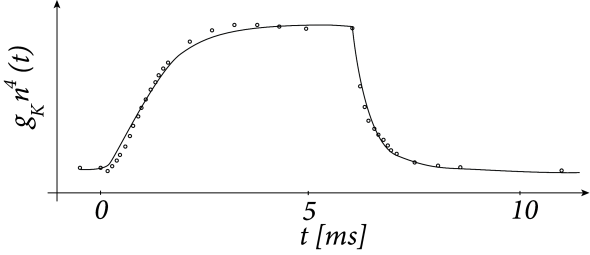
A classic example is the Hodgkin–Huxley (HH) model, which remains the foundation for most neuron-level biophysical models. It mathematically describes how ion channels in a neuron’s membrane open and close in response to voltage changes, generating the rapid rise and fall (spike) of the membrane potential. It links the flow of sodium and potassium ions to the cell’s voltage, accurately capturing the timing and shape of real neuronal action potentials.
An EE way of displaying the Hodgkin Huxley equations Implicitly, to be understandable, the components must be simple enough, and to let us understand their interactions at the higher level, the function they jointly implement must not be too complex. Because the resulting ways of thinking are either in terms of word models or in terms of simple mathematical models, the underlying relations must be relatively simple.
We can experimentally identify the components and their interactions. It is generally assumed that we can run experiments to understand how these components interact. For example, we might see the ion channels under a microscope and probe them with patch-clamp recordings. Similarly, we might visualize neurons in a microscope and probe their interactions using optogenetics.
Comparing predictions with actual behavior. Once we understand the components, we can test whether our resulting models are good at describing system behavior at a higher level. We justify a model by showing that insights at the lower level accurately predict what happens at the higher level.
Hodgkin Huxley is good at fitting (some) neuronal responses, Insights from a good fit. When the model accounts well for behavior, we gain multiple insights:
Our assumptions/measurements about the components may be good.
Our assumptions/measurements about their interactions may be good.
We can make predictions about how perturbations will affect the system.
We understand relations across levels of scale.
Ultimately, understanding mechanism promises us the ability to predict the result of interventions, the ultimate goal of medicine.
Scales
Mechanistic models exist at all levels of scales. A biological molecule '“works” because of interactions between its atoms - e.g. in the case of how a Sodium channel can produce a current. Almost all phenomena appear to have a bottom level of physics. Axons “work” because of the involved channels. Neurons “work” because of dendrite-soma-axon interactions. Local microcircuits2 may work because the interactions between neurons. Brain areas may work because of the interactions of microcircuits. And brains may work because of the interactions between brain areas. Behavior may work because of brain-bodypart interactions. And societies work because of human-human interactions. At all these scales do we build mechanistic models and on all of the scales the logic seems to be the essentially the same.
Normative thoughts matter (but not here)
Neuroscientists sometimes criticize mechanistic models for not providing insights about why the system has various properties, what these properties are useful for. For example, finding a certain neural structure or a particular set of ion channels does not tell us why it is useful for an animal to have these. However, many mechanistic studies are inspired by normative ideas. For instance, someone studying the mechanisms of visual processing may start with the assumption that the brain should extract edges from real-world stimuli because edges are crucial for many tasks.
What to do when the underlying component interactions are not simple?
In standard mechanistic models, we strive for human-understandable equations. However, as interactions within a system become too numerous or diverse, simplifying them into a small number of human readable equations becomes infeasible. In these scenarios, there are so many equations with so many parameters that the only way to really dealing with this is large-scale simulations. However, in relatively small systems like C. elegans such simulations should now be possible.
Mechanistic models can feel extremely powerful at the scale of single neurons or synapses yet can become unwieldy at the scale of many neurons or synapses with many relevant ion channels. The computational complexity balloons, and the resulting equations can no longer be understood by mere mortals. If we are to believe in the promise of mechanistic understanding, we may still have to leave the space of human-understandable models.
Mechanistic models are the best we can currently do for many microscopic neuronal properties
In mechanistic models, there is a link between experiments at one level (e.g. neurons) and experiments at another level (e.g. behavior). This allows a unique way of predicting data and provides a sanity check for our understanding. Moreover, by design, mechanistic models predict how perturbations will change behavior—essential for medical interventions. The logical link between layers is clear, it is experimentally addressable, and the “glue” between the layers is typically a modeling effort. Mechanistic models are currently the workhorse of neuroscience.
The field of binding by synchrony, despite my initial excitement about it, went through a bubble and eventually ended up not convincingly describing how the brain mechanisticaly binds information. I now see strong similarities of that field with various fields that are hype now.
I need to add a short description why I use may here. I think that we have well established that there are meaningful questions where we can separate models of neurons from models of the surrounding tissue (e.g. for spiking). For higher levels of abstraction, like microcircuits, it is less clear to which level they can actually be meaningfully modeled as a somewhat independent component from all the rest.
This is great Konrad, and I would add one more advantage of such models, which is that they can expand our intuitions about how complex systems work, and this in turn allows for the cognitive development of new ideas that wouldn't have been possible otherwise. As an example, deep learning has made it possible to think more clearly about how simple ideas can scale up. We already had the core idea of interacting layers of feature detectors with the pandemonium model from many decades ago, but when we first developed image computable models such as Alexnet (and for me the early work Riesenhuber, Serre & Poggio did this) , our intuitions as scientists were expanded. This upgrade has substantially changed the way that vision scientists are approaching their work by allowing us to think more concretely about image processing rather than being limited to simple feature processing.
Of course there were vision scientists who thought about image processing before deep learning (e.g. Aude Oliva, Mary Potter), but they were in the minority. Image work in human vision science is now rapidly becoming mainstream, not just with modellers but also with experimentalists.
> Mechanistic models can feel extremely powerful at the scale of single neurons or synapses yet can become unwieldy at the scale of many neurons or synapses with many relevant ion channels. The computational complexity balloons, and the resulting equations can no longer be understood by mere mortals. If we are to believe in the promise of mechanistic understanding, we may still have to leave the space of human-understandable models.
When we have huge mechanistic models that are no longer human-understandable, they start to feel like DNNs in the sense that "understanding" amounts to prediction and perturbation/ablation analysis (maybe there is more?). Is the only difference then that large mechanistic models have building blocks that are more biologically plausible than DNNs?