Normative models of plasticity

or: How I learned to stop worrying and love the gradient

Advances in both neuroscience and computational theory have deepened our understanding of learning and adaptation, yet the intricate process of synaptic plasticity remains a fascinating enigma. Synaptic plasticity—the mechanism by which neurons modify their connections in response to experience—is fundamental to learning and memory. Despite its critical role, the diversity of plasticity phenomena poses a significant challenge: How do these varied processes work together to support efficient and robust learning? In this post, we adopt a normative framework that bridges computational insights with biological realities. By considering the brain as a high-dimensional system optimized by evolution, we explore how seemingly disparate plasticity mechanisms might converge to solve the complex problem of learning in a dynamic world. In what follows, I will show how framing plasticity in terms of normative principles not only unifies diverse phenomena but also offers testable predictions for both neuroscience and computational models.

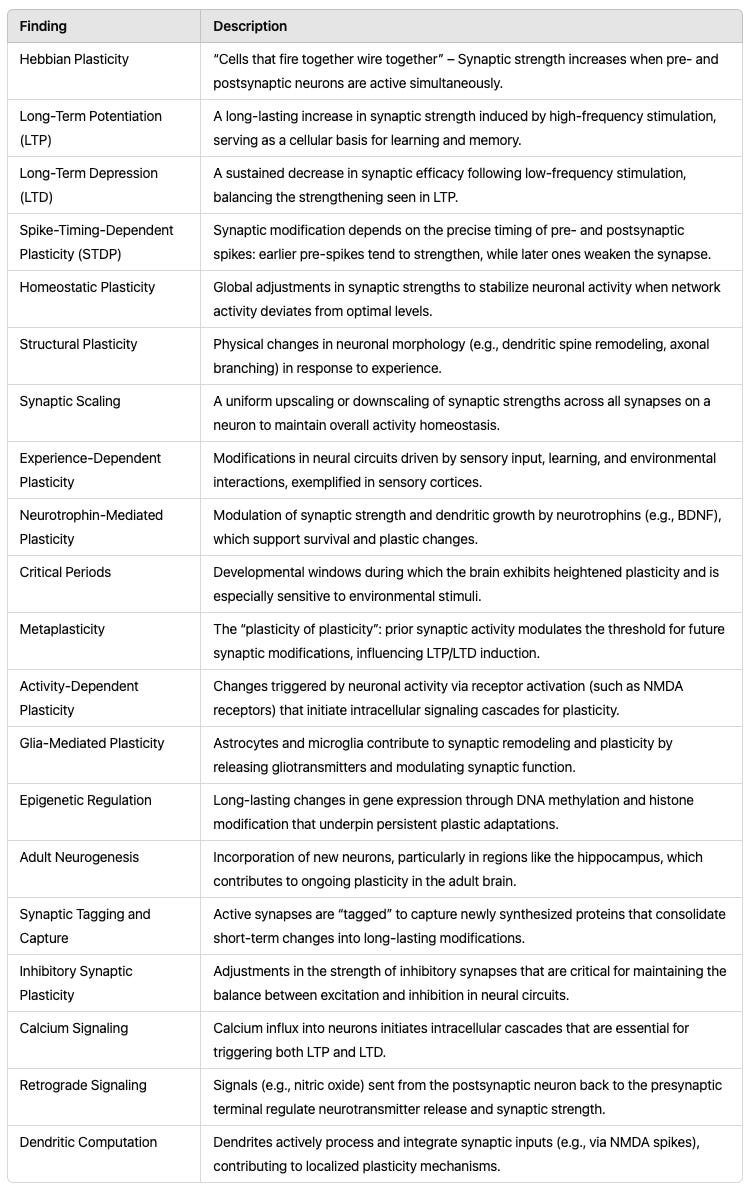
Plasticity, defined as how neurons change over time, in particular during learning, is one of the main branches of neuroscience. When we look at plasticity, we find a massive zoo of established effects. This ‘zoo’ is a vivid metaphor for the extensive and diverse mechanisms that have evolved, each contributing unique yet overlapping roles in learning.

A very partial table of known plasticity effects.

So we have countless known ways how neurons work. How can we possibly believe that they all constructively work together, enabling us to learn well in a complicated world. The diversity of plasticity effects is so massive that it seems almost unthinkable for us to truly understand how animals actually learn, that we could understand how plasticity allows intelligence. We may thus be well inclined to believe in a remarkably efficient blind watchmaker - or a divine presence, depending on ones’ persuasion.

Normatively Thinking About Plasticity

If we start with a stance of taking evolution seriously, we should believe that plasticity, despite being so multifaceted, ultimately is well adjusted to allow successful behavior in a complicated world. And I believe that out of this realization already we can derive a lot about how plasticity should be orchestrated to allow animals to learn so well. This perspective assumes that evolution has finely tuned neural mechanisms, meaning that every plasticity process serves a specific, efficient function in adapting to our environment.

Let's dive into a normative framework for understanding plasticity. This will mean that we want to list aspects about the niche where we evolve and learn, and derive from those aspects what we should expect to be true about brains.

The Brain must be high dimensional

Niche: For all practical purposes in our lives the world is infinite dimensional. My office probably contains thousands of objects. My building may contain millions. There are said to be thousands of species of bacteria living in each of our bodies, with some estimating trillions of species on our planet. There are supposed to be more than 7 million species of animals on this planet and about 10²⁵ planets. In other words, the outside world is incredibly large and even the tiny sliver of the outside world that matters for our behavior is indescribably large. Here, ‘infinite dimensional’ is not literal but reflects the staggering diversity of variables the brain must represent and manage.

Normative insight: If so many variables can matter for our behavior, then there is no doubt that the brain should be such that it can represent these variables. Which, in turn, implies that the brain must be very high dimension. Indeed, this prediction is borne out by the fact that the human brain comprises roughly 10^11 neurons connected by about 10^14 synapses, underscoring its immense representational capacity.” The brain is high dimensional.

The Brain must learn in a high dimensional way

Niche: Each synapse represents at least a few parameters that can probbly be modified through experience. There are a very large number of the. These parameters must be matched to the outside world.

Normative insight: To properly represent the incredibly large world around us, these synapses must have the right values and to do this, they must acquire that knowledge about the world from our environment. This process is akin to a high-resolution camera sensor finely tuning each pixel to capture the intricate details of a scene, thereby constructing a detailed internal model of the world. Therefore, there must be a mechanism that adjusts all these parameters during our lives - a mechanism we call plasticity. The high dimensionality plastical system then has tremendous representational capacity, allowing for complex internal models of the world.

The Efficiency Imperative

Niche: Given this high-dimensional space, biological learning must be efficient. Evolution selects for organisms that can learn quickly with minimal resources. A learning algorithm that requires exhaustive search of the parameter space would be biologically implausible.

Consider the alternatives:

1. Random search of parameter space? Computationally intractable. It literally grinds to a halt as we make the system higher dimensional.

2. Evolutionary algorithms? Too slow for within-lifetime learning because they are just a version of random search.

3. Reinforcement learning alone? Sample inefficient.

4. Any zeroth order optimization algorithm? Hopelessly inefficient.

Animals have a lifetime that is much shorter than the number of relevant parameters in the environment. Therefore, efficient learning in high dimensions requires methods that scale well. This constraint forces the brain to evolve rapid, resource-efficient strategies that can optimize learning without exhaustively testing every possibility.

The Gradient Necessity

Normative insight: This brings us to gradients. Gradient-based learning represents the most efficient known method for optimizing high-dimensional systems. By computing how small changes in each parameter affect the overall performance, the system can update parameters in directions that improve performance and it can update all of them at the same time. For example, backpropagation in deep neural networks mirrors this process by efficiently propagating error signals to update every parameter simultaneously. Indeed, we have recently argued that the massive zoo of plasticity phenomena can be understood as just special cases of doing gradient descent.

The Gradient Possibility

All the arguments I made above are moot if, for biological systems, it is impossible to evolve gradient-like performance. However, a growing body of research shows that gradient descent is achievable in models that closely mirror biological processes. For instance, burstprop mechanisms—illustrated by studies from my PhD and e.g. work by Richard Naud—demonstrate that bursts of action potentials can effectively propagate gradient signals through neural circuits, thereby approximating the function of gradient descent. Similarly, the predictive coding framework posits that the brain continuously generates predictions about sensory inputs and then refines its internal models based on the ensuing prediction errors, a process that can implement gradient descent. There are algorithms related to recurrent symmetrical systems, e.g. eqprop. There is even, meta learning—where neurons essentially learn how to learn. Together, these approaches collectively illustrate that biological systems could clearly do gradient-like optimization with the kind of hardware they have.

Moreover, this framework not only advances our theoretical understanding but also opens new avenues for exploring neurological disorders where deviations from gradient-like optimization may play a role.

Further Normative Implications

Normative thinking gives rise to many insights about plasticity in brains, and I want to just mention a few more.

1. Structured representations are needed. The high-dimensional structured nature of biological learning means that representations must be structured to be manageable. This suggests hierarchical organization, sparse coding, and modularity should emerge naturally.

2. Multi-timescale learning is needed. For instance, rapid synaptic modifications may capture immediate changes in the environment, while slower adjustments could encode long-term patterns, reflecting the diverse temporal demands of our experiences.

A concrete example of successful predictions

There are many links between normative models and physiology For example, Hebbian learning converging to the dimension of maximal variance in the input, arguably the most interesting aspect of data. But I want to give an example here where normative predictions far preceded and predicted physiological measurements. Martin Taylor, in 1973, realized a problem in training a large number of neurons to respond to time-varying inputs: there needed to be a mechanism that makes sure neurons get tuned to distinct stimuli. He suggested that in this domain the right solution was to have neurons strengthen inputs from neurons that fire before them and weaken connections from neurons that fire after them. Indeed, Yang Dan and Mu-Ming Pu found exactly that pattern in neural data. More recently, there is deeper normative work, showing that a different information related criterion, Bayesian estimations lead to STDP as optimal solution.

Conclusion

Normative thinking lets us connect the properties of the niche in which we live to expected properties of brains and brain-like artifacts. It allows a broad set of predictions that are still not mainstream in neuroscience. As we continue to unravel the mechanisms of plasticity, keeping these normative principles in mind will guide our understanding of how brains learn and adapt. The mathematical imperatives of high-dimensional learning constrain the possible implementations of plasticity, pointing us toward a deeper understanding of biological learning. The beauty of this approach is that it bridges computational theory with biology, revealing the elegant solutions evolution has discovered for the fundamental problem of learning in complex, high-dimensional spaces. Future research that embraces these normative principles may not only deepen our understanding of biological learning but also inspire innovative approaches in artificial intelligence and clinical neuroscience.