Attractors are usually not mechanisms

The mathematical objects can not be. And the "attractor models" have not been established as mechanisms in mammals

Mathematical attractors elegantly formalize stability and convergence, but in neuroscience the term is often mistaken for a full mechanistic explanation. Demonstrating bump‑like activity in head‑direction circuits shows the phenomenon, not the cause; the required Mexican‑hat connectivity, biophysical dynamics and precise organization remain unverified. Generic recurrent networks, trained without explicit ring structure, replicate all hallmark behaviors—convergence, persistence, smoothness, lesion effects—undermining claims that attractors are necessary. True mechanistic proof demands write‑in perturbations, quantitative connectivity maps, bifurcation‑grade parameter sweeps and falsification of RNN alternatives. Until such experiments succeed, attractors are appealing hypotheses, not established mechanisms. Maintaining rigor will drive genuinely explanatory neural science.

Within mathematics attractors are well defined

Attractors are beautiful. Let me define them as:

An attractor is a subset A of the system's phase space such that:

1. Forward invariance: Once the system's state is in A, it stays in A for all future time.

2. Attraction (basin of attraction): There exists an open neighborhood B(A) ("basin") of initial conditions so that every trajectory starting in B(A) asymptotically approaches A as time t→∞.

3. Minimality: No proper subset of A satisfies (1) and (2).

This definition is beautiful in its abstraction—it captures the essence of stability and convergence without specifying any particular mechanism. They also align with normative ways of thinking. In a way this would be great if the way we handle belief worked like this - we may converge to true belief states - which we don’t always because of uncertainty etc but lets take for granted that having attractor like things in our heads might be useful for some things.

Attractors as rather a specific model type in neuroscience

Concept of an attractor for continuous variables (source). A truly elegant model. Is this *the* mechanism?

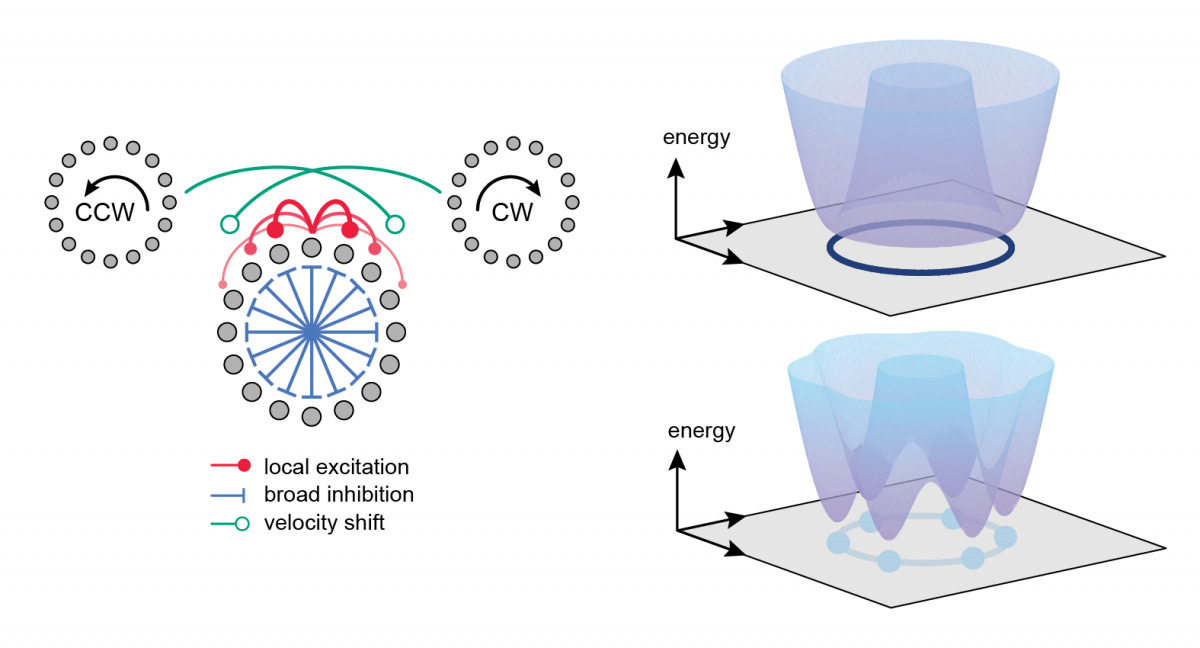
Now, our model’s are not merely what the math above says, they are much more narrowly defined. Lets rather go through a standard type of that model. Picture a continuous attractor network where neural activity forms a "bump" of firing that can sit anywhere along a ring of neurons:

\(\begin{align} \tau \,\frac{d h_i}{dt} &= -h_i \;+\;\sum_{j} W_{ij}\,r_j \;+\; I_i \;+\; \eta_i(t), \\[6pt] r_i &= f\bigl(h_i\bigr), \\[6pt] W_{ij} &= A\,\exp\!\biggl(-\frac{|i-j|^2}{2\sigma_E^2}\biggr) \;-\; B\,\exp\!\biggl(-\frac{|i-j|^2}{2\sigma_I^2}\biggr). \end{align} \)

Where h_i is the synaptic input to neuron i, r_i is its firing rate, W_ij encodes Mexican-hat connectivity (local excitation A with narrow width σ_E, broad inhibition B with width σ_I), I_i is external input, and η_i(t) is noise. When the parameters are tuned just right, you get a stable bump that can live anywhere on the ring - a continuous attractor.

Model behavior: The system's state space contains a curve (the "ring attractor") where activity naturally flows and stays. Perturb the bump slightly? It slides back to the manifold. Push it along the ring? It glides smoothly to a new stable position. It's like having a marble rolling on the inside of a perfectly circular tube—stable, continuous, gorgeous. This gives you angular integration for free. Velocity input shifts the bump, the bump persists when input stops, and you've got a neural compass. The same equations explain persistence, integration, and stability (but they also basically have specialized components for each of these). However, this mathematical description tells us about the dynamics, not the mechanism.

To say things clearly, the attractor is a property of the system's behavior, not an explanation of how that behavior arises from biological components. Any number of different mechanisms could give rise to such observations.

What the word Mechanism means

In the mechanistic philosophy of science, e.g. Bechtel, Craver, Ross and Bassett etc, a mechanism consists of:

Entities and activities organized in a way that produces a phenomenon.

Entities are the parts (neurons, synapses, circuits). Activities are what they do (spike, release neurotransmitter, integrate signals). The organization is how they're arranged spatially, temporally, and causally to create the phenomenon you're trying to explain.

For attractors, this means you need:

• Entities: Specific neurons with specific connectivity patterns

• Activities: The actual biophysical processes that create Mexican-hat dynamics

• Organization: The precise spatial and temporal arrangement that generates the attractor manifold

Showing that your system has attractor-like behavior is not the same as demonstrating the attractor mechanism. It's like seeing a car drive smoothly and concluding it must have a rotary engine you've identified the phenomenon, but misidentified the mechanism.

The Head-Direction System: The cleanest

Let's talk head-direction, the poster child for neural attractors. These neurons fire when an animal faces specific directions, creating a neural compass that persists in darkness and integrates angular velocity. If attractors exist anywhere in the mammalian brain, it's here.

The evidence looks compelling:

• Ring-like manifold: Population activity lives on a circle in neural state space

• Multi-area necessity: Lesion LMN, ADN, or PoS and the compass breaks

• Zero-lag coherence: Cells across areas fire in tight synchrony

• Angular integration: The system tracks head turns even without visual input

Beautiful, right? But is this convincing to argue that the kind of model discussed above lives in the circuit?

The Missing Entities: We don't have the anatomically-mapped connectivity matrix. We do have e.g. the Drosophila connectome but it comes without weights and many interactions will be non-local/ Show me the Mexican-hat profile—the precise excitatory neighborhoods and inhibitory surrounds that the math demands and that could elevate it to a mechanism. We have hints (reciprocal connections between ADN and LMN, broad inhibition in local circuits), but not the quantitative weight profile that would prove W_ij matches the equations.

The Missing Activities: We don't know if the biophysical dynamics actually implement continuous attraction. Maybe it's just a learned lookup table. Maybe it's predictive coding. Maybe it's something weirder. The equations describe the phenomenon but the phenomenon does not necessitate the equations.

The Missing Organization: Even if we had the right connectivity, we'd need to show that this specific organization is what creates the phenomenon—not just that it's compatible with it.

The Non-Attractor Alternative

You can build a perfectly functional head-direction system without any simple attractor dynamics at all using an RNN. Take a vanilla recurrent neural network. No Mexican hats, no ring topology, no continuous manifolds. Just:

\(\begin{equation} h_{t+1} \;=\; \tanh\!\bigl(W_{\mathrm{rec}}\,h_{t} \;+\; W_{\mathrm{in}}\,u_{t} \;+\; b\bigr) \end{equation}\)

Where h_t is the hidden state, u_t is angular velocity input, W_rec and W_in are learned weight matrices, and b is bias. Train it on angular integration using standard backpropagation through time.

What happens? The network works. It:

• Converges to stable representations

• Persists activity without input

• Integrates angular velocity smoothly

• Even develops a ring-like manifold when you do PCA on the hidden states

The network learns to approximate the attractor dynamics through pure optimization, with no fancy mathematical structure built in. It's ugly, it's generic, it's completely un-principled—and it passes every behavioral test we throw at biological head-direction systems.

Worse yet, this RNN will show "lesion" effects too. Damage random connections and performance degrades. Knock out specific hidden units and you get direction-specific deficits. The ugly duckling mimics the swan perfectly.

In fact, fitting RNNs make attractors when data do not have attractors

We record a tiny part of the overall brain. A popular approach to study brain data is to fit an RNN to neural data and then show that this RNN has attractors. However, a recent paper showed that in the context of partial observations, a simulated system that has no attractors gives rise to a fitted RNN that does have attractors. In other words, in the context of unobserved data (always the case in neuroscience), we may even wrongly infer that there are attractors. Mechanism is an illusion in these cases.

Four Behaviors Every Model Must Show (The Minimum Bar)

Any model that explains head-direction behavior—attractor or not—must exhibit:

Convergence: The system needs to settle on a single direction estimate, not flutter between multiple interpretations, it needs to be noise and perturbation tolerant.

Persistence: The direction signal must maintain itself when angular velocity input stops.

Smoothness: Biological trajectories are always low-pass; systems do not jump discontinuously.

Predictability: The dynamics must be orderly enough to forecast future states from current ones.

But any competent model will show these four features automatically. Your attractor network displays them? Congratulations, you've met the basic requirements. The ugly RNN shows them too, for the same reasons—they're necessary properties of any system that solves the task.

This is not evidence for a specific mechanism; it's evidence that your model isn't completely broken.

Lesion Logic ≠ Mechanism

"But we lesioned LMN and head-direction tuning collapsed! The attractor must live there!" This is a natural conclusion, but let's think it through. Destroy your car's carburetor and the engine stops, but that doesn't tell you whether it's four-stroke, rotary, or powered by some other mechanism entirely. Causal necessity (LMN is required) is not the same as causal sufficiency (LMN implements the attractor).

All we know is that LMN is part of the causal chain. Maybe it's the attractor substrate. Maybe it's the input preprocessor. Maybe it's the output formatter. Maybe it's the computational bottleneck that makes any direction system collapse when damaged. The lesion tells us where the system breaks, not how it works when intact.

We need a Write-In Experiment

The Drosophila folks optogenetically create artificial "bumps" in the ellipsoid body—the fly's compass—and watch them behave exactly like natural ones. Zap one location, conjure a false direction signal, and the fly acts as if it's facing that direction. That's causal sufficiency: the ability to write in the phenomenon, not just break it. Still not necessarily sufficient evidence but much stronger.

In the mammalian brain things look much worse. We can lesion the head-direction system in a dozen ways, but nobody has dragged a rodent's direction bump around in closed loop. Until someone can write artificial bumps into LMN and watch them propagate through the circuit like real ones, the evidence is super slim

Checklist for a Real Attractor Claim

Here is a minimum I expect:

1. Write-in experiments: Artificially create bumps and show they behave like natural ones

2. Anatomical weight mapping: Measure the actual connectivity profile and show it matches the Mexican-hat equations

3. Bifurcation-grade perturbations: Tune parameters across the theorized phase transitions and watch the system reorganize as predicted

4. Falsification of alternatives: Show that generic RNNs can't match the system's behavior under the same perturbations

And point (4) is probably infeasible in basically all cases.

Why This Matters

Precise mechanistic claims matter for more than just academic rigor. They guide experiments, focus research programs, and help us build cumulative knowledge. When we get sloppy about the word "mechanism," we risk losing our ability to distinguish genuine explanations from elegant descriptions.

If every stable neural trajectory becomes an "attractor," the word stops being informative. If every learning algorithm that works becomes "biologically plausible," we've diluted the concept beyond usefulness. We need sharper conceptual tools because better concepts lead to better science.

A Call for Exciting Experiments

Instead of just celebrating simulations that look right, let's run the really interesting experiments—the ones that can actually distinguish between competing explanations:

• Closed-loop perturbations: Design stimulation protocols that can tell attractor dynamics apart from learned approximations

• Comparative benchmarks: Test your elegant attractor against ugly-but-effective RNNs on identical tasks

• Parameter sweeps: Push the system across theorized bifurcation points and see if it reorganizes exactly as the math predicts

• Write-in challenges: Create artificial activity patterns and test whether they propagate like natural ones

If the attractor mechanism survives that gauntlet, fantastic—we've discovered something profound about neural computation. If it doesn't, we've still learned something valuable instead of polishing a beautiful theory that happens to be incomplete.

Conclusion: Let's Earn Our Mechanistic Explanations

Attractors as used by neuroscientists might be fundamental to neural computation. The mathematics is genuinely elegant, the behavioral fits are compelling, and the intuitions feel deeply right. But "feeling right" isn't the same as "being right," and behavioral compatibility isn't the same as mechanistic explanation.

Mechanisms are earned through careful work, they require entities, activities, and organization, not just equations that fit the data. Until we can write in the bumps, map the connectivity precisely, and navigate the predicted bifurcations, we're in the exciting business of hypothesis testing, not yet in the satisfying business of mechanism explaining.

The evidence so far? Promising but rather preliminary. Let's keep building toward the real mechanistic understanding and keep the standards high enough that when we finally get there, we'll know it was worth the effort. It is time to plan the experiments and to check theoretically how we can even distinguish generic RNNs from the model class we call attractors.